knn
KNN算法思想:如果一个样本在特征空间中的 k 个最相似的样本中的大多数属于某一个类别,则该样本也属于这个类别 。主要解决分类问题。
knn是一个不需要训练的算法。 没有模型的算法。 为了和其他算法统一,knn训练数据集就是模型本身。
knn特点:
- 效率比较低,m 个样本 n 列,o(m*n) 。
- 预测结果不具有可解释性的特点。
距离
https://blog.csdn.net/weixin_41620451/article/details/105918973
- 曼哈顿距离
- 欧拉距离:
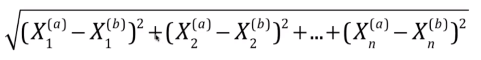
- 搜索明可夫斯基距离相应的p
拆分数据集
将数据拆分乘 测试集和训练集
测试算法
1sum(y_predict == y_test) / len(y_test)
网格搜索
数据缩放
归一化
把数据都映射到 0-1中。
1x_scale = (x - min(x)) / (max(x) - min(x))
如果数据很不规整,有很大的极大值,和极小值, 那么这种数据采用这种方式,会使数据不准确。
标准化
1s = np.std(x)
2x_scale= (x - x_mean) / s
线性回归
线性回归(Linear regression)是利用 回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关系进行建模的一种分析方式。
- 只能解决回归问题
- 其他非线性模型的基础
- 结果具有很好的可解释性
- 蕴含机器学习中的很多重要思想
- 典型的参数学习
一元线性回归
- y = kx +b, 目标值只与一个因变量有关系
多元线性回归
- y(w) = w1x1 + w2x2 + w3x3 + … + wnxn + b
简单线性回归
假设我们找到了最佳拟合的直线方程
y=ax+b
则对于每一个样本点x(i) , x的第i个特征
根据我们的直线方程,预测值为: ^y(i) = a*x(i)+b
表达式 ^y(i) 和 y(i) 的差距: (^y(i) - y(i))^2
目标:找到 a和 b 使得 所有 (y(i) - a*x(i)- b)^2 的和最小 (损失值)
损失值也叫损失函数、效用函数。
通过分析问题,确定问题的损失函数或者效用函数
通过最优化损失函数或效用函数,获得机器学习的模型
衡量线性回归法的指标
损失函数
最小二乘法: 误差平方和
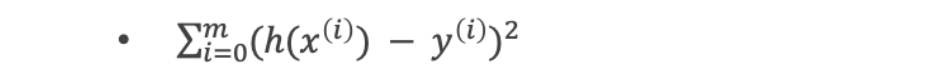
均方误差(MSE,mean-square error)
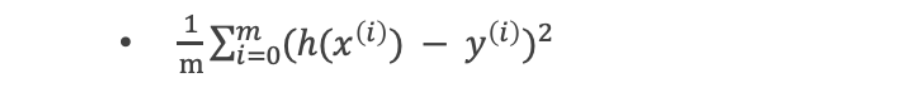
均方根误差(RMSE)
MSE^1/2 ,上面的开根号
平均绝对误差值(mean absolute error,MAE)
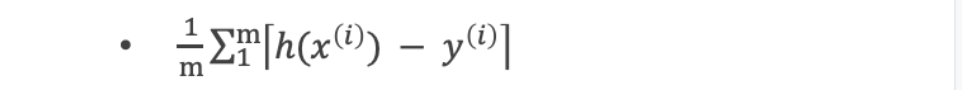
最小二乘法
最小二乘法: 公式(过程暂时忽略)
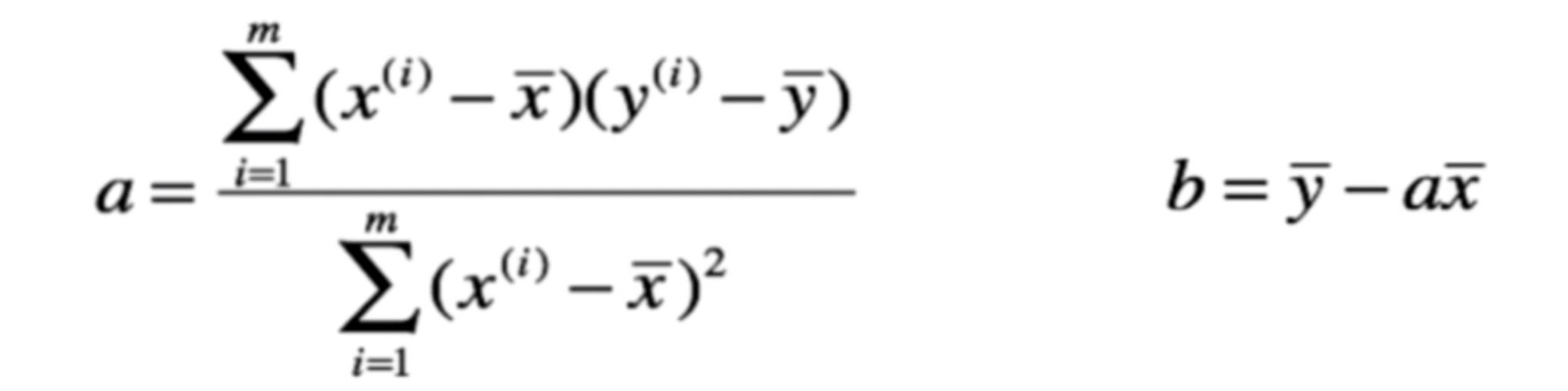
向量化运算
最好的衡量线性回归法的指标 R squared
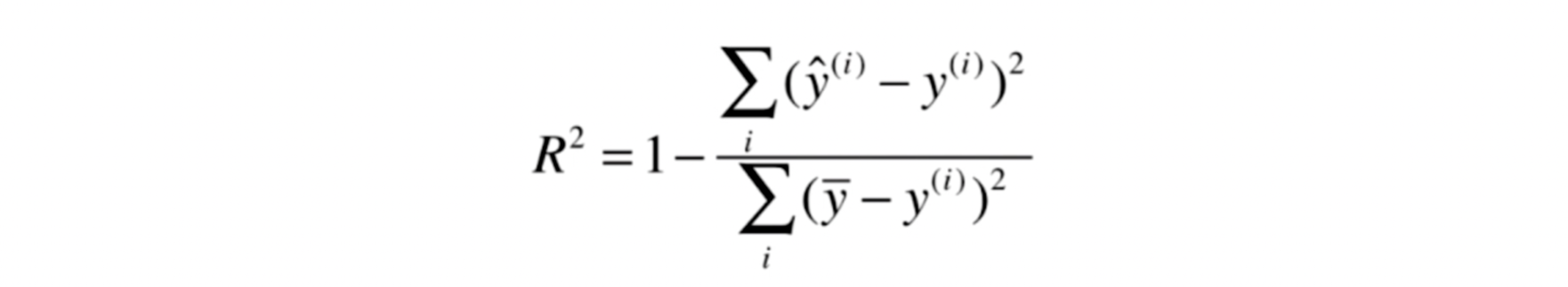
多元线性回归
正规方程法 时间复杂度较高 o=(n^3) ,行数、列数太多,都不合适。
正规方程法
以下是公式推导过程:
设定 theta0=就是截距
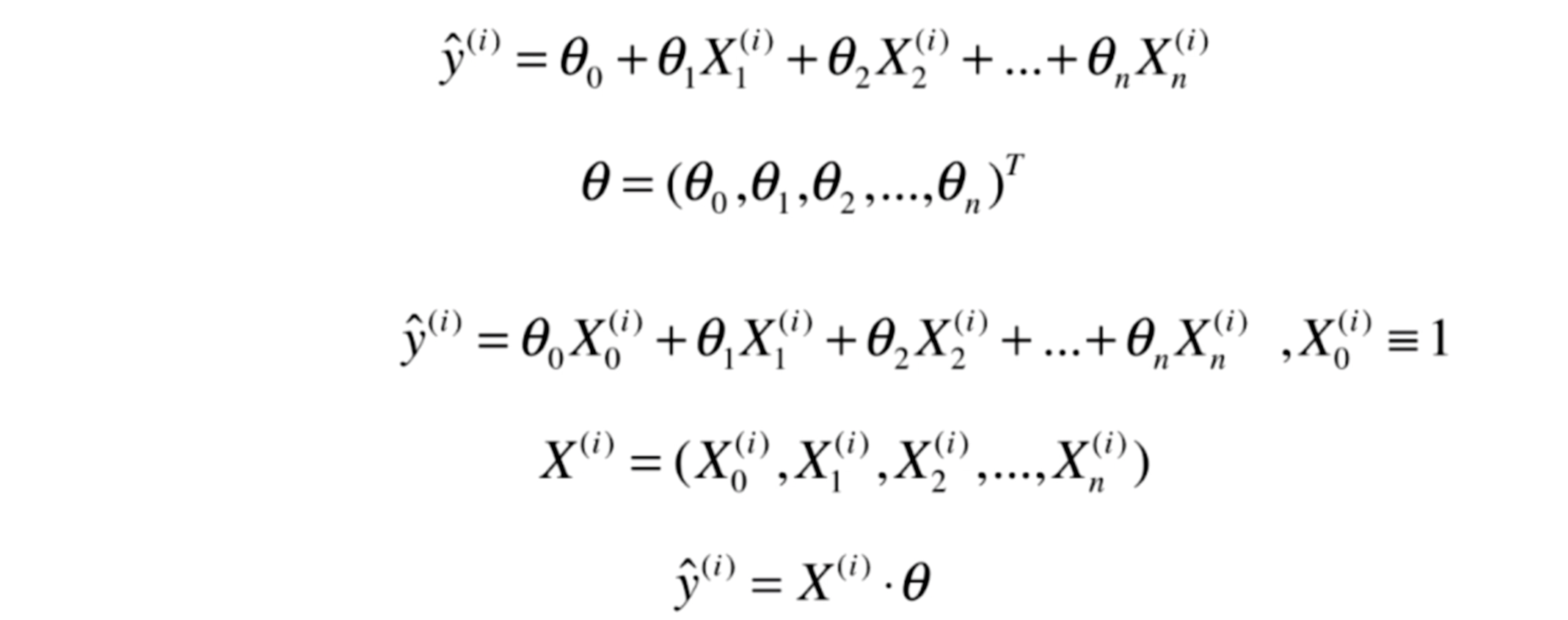
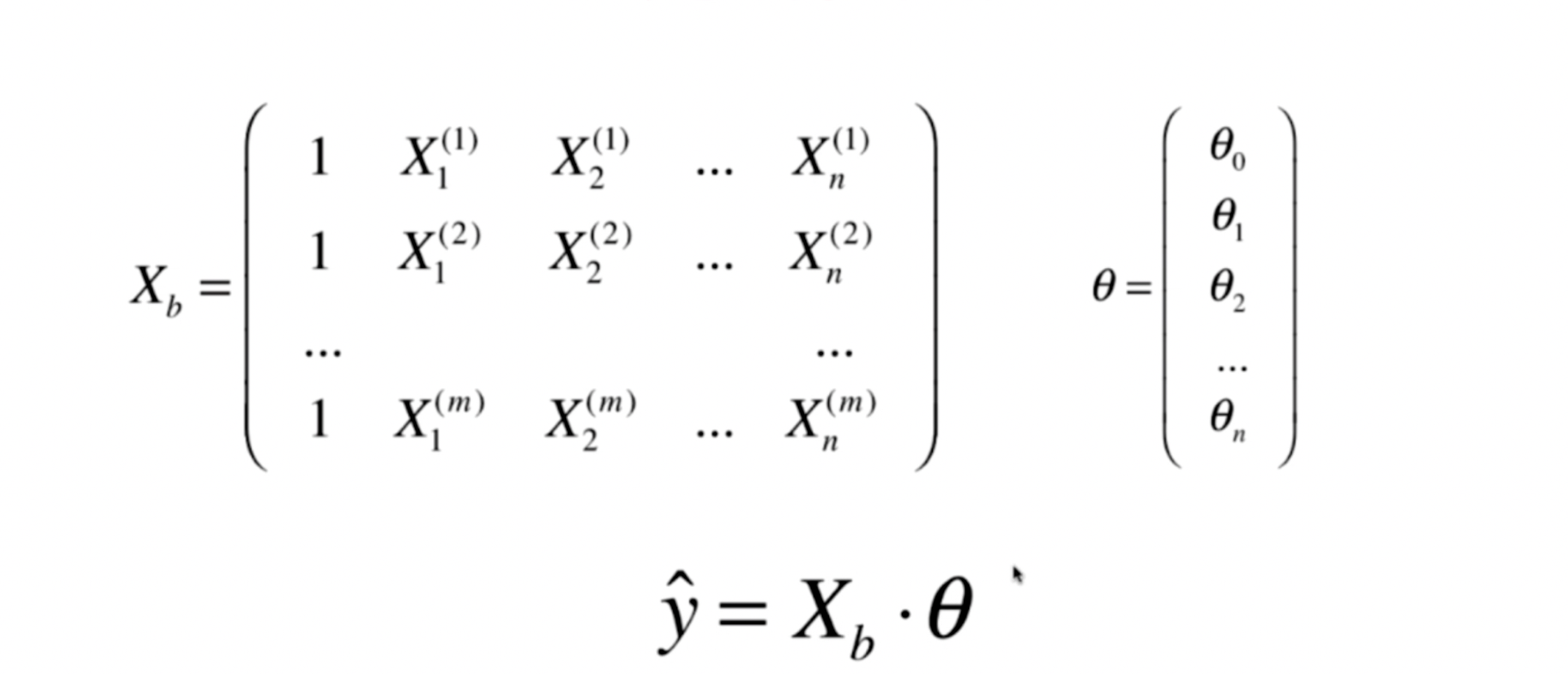
矩阵的乘法公式: 就是 xT . x =x1^2+x2^2+…xm^2, 就是下面公式就是 l2范数的平方 (其中x是长度m的向量)

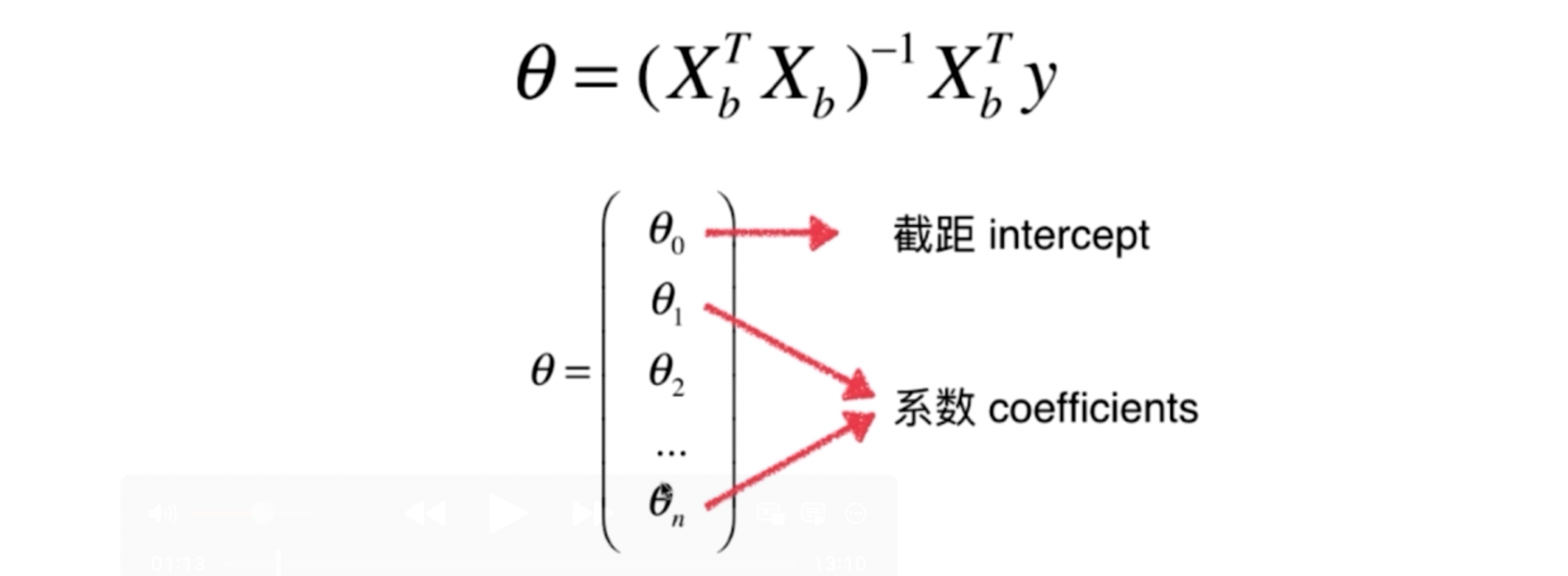
实现过程
1import numpy as np
2from .metrics import r2_score
3
4
5class LinearRegression:
6
7 def __init__(self):
8 """初始化Linear Regression模型"""
9 # 系数
10 self.coef_ = None
11 # 截距
12 self.intercept_ = None
13 # ^y = Xb * _theta 都是向量运算
14 self._theta = None
15
16
17 def fit_normal(self, X_train, y_train):
18 """根据训练数据集X_train, y_train训练Linear Regression模型"""
19 assert X_train.shape[0] == y_train.shape[0], \
20 "the size of X_train must be equal to the size of y_train"
21 # 填充 为值 1 的 ,行数为len(X_train)的,一列 的向量
22 X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
23 #np.linalg.inv求逆, 就是图片中的shu'xue'fu'hao
24 self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
25 # 截距
26 self.intercept_ = self._theta[0]
27 # 系数
28 self.coef_ = self._theta[1:]
29
30 return self
31
32 def predict(self, X_predict):
33 """给定待预测数据集X_predict,返回表示X_predict的结果向量"""
34 assert self.intercept_ is not None and self.coef_ is not None, \
35 "must fit before predict!"
36 assert X_predict.shape[1] == len(self.coef_), \
37 "the feature number of X_predict must be equal to X_train"
38 # 给 x 追加 截距
39 X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
40 # ^y = Xb * _theta 都是向量运算
41 return X_b.dot(self._theta)
42
43 def score(self, X_test, y_test):
44 """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
45
46 y_predict = self.predict(X_test)
47 return r2_score(y_test, y_predict)
48
49 def __repr__(self):
50 return "LinearRegression()"
对于theta 因子的思考
大于0 表示 正相关, 小于0表示负相关。
如房价,利于房价的特征(因素), 不利于的房价的特征
多项式回归与模型泛化
什么是多项式回归
线性回归模型不能很好的拟合预测数据, 通过增进特征项来达到拟合。
scikit-learn中的多项式回归
poly = PolynomialFeatures(degree=2)
就是最高增加2次幂的特征
如有2个特征x1,x2 ,那么会增加4列:
- 全是1的(0次幂)
- x1^2
- x2^2
- x1*x2
poly = PolynomialFeatures(degree=3), 就是最高增加3次幂的特征 x1,x2 -> 1,x1,x2,x1^2,x2^2,x1x2,x1^3,x2^3,x1^2x2,x2^2*x1
欠拟合与过拟合
过拟合:一个假设 在训练数据上能够获得比其他假设更好的拟合, 但是在测试数据集上却不能很好地拟合数据 (体现在准确率下降),此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合:一个假设 在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据 ,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
解决方案:L1正则化、L2正则化
欠拟合
欠拟合产生原因: 学习到数据的特征过少
解决办法:
-
添加其他特征项,有时出现欠拟合是因为特征项不够导致的,可以添加其他特征项来解决
-
添加多项式特征,模型过于简单时的常用套路,例如将线性模型通过添加二次项或三次项使模型泛化能力更强
过拟合
过拟合产生原因: 原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾所有测试样本
解决办法:
- 重新清洗数据,导致过拟合的一个原因有可能是数据不纯,如果出现了过拟合就需要重新清洗数据。
- 增大数据的训练量,还有一个原因就是我们用于训练的数据量太小导致的,训练数据占总数据的比例过小。
- 模型正则化
- 减少特征维度;降噪
- 降低模型复杂度
- 使用验证集
学习曲线
随着训练样本的逐渐增多,算法训练出的模型的表现能力。
根据样本数的增进,看分数值(误差值) 的图 观察,欠拟合、欠拟合,正好拟合的情况。
验证数据集与交叉验证
- 训练数据集 (产模型)
- 验证数据集 (产模型)
- 调整超参数使用的数据集
- 测试数据集
- 作为衡量最终模型性能的数据集。
K交叉验证
推荐用这个。 这个得到的结果才是最好拟合的。
原理就是将数据集合分成k份 ,将k-1份数据进行训练,重复k次,每个子级都会被当成测试集 。通常我们会取k次验证的平均值作为最终性能指标。
缺点就是: 相对慢了k倍.
偏差方差平衡
- 偏差: 里正确目标的差
- 方差: 结果之间的差距
模型误差 = 偏差 + 方差 + 不可避免的误差
导致偏差的主要原因:
-
对问题本身的假设不正确
- 如:非线性数据使用线性回归
- 如 欠拟合underfitting
-
有一些算法天生是高方差的算法。如knn。
-
非参数学习通常是高方差算法。因为不对数据进行任何假设
-
有一些算法天生是高偏差算法。如线性回归。
-
参数学习通常都是高偏差算法。因为堆数据具有极强的假设。
偏差和方差通常是矛盾的,降低偏差会提高方差,降低方差,会提高偏差。
机器学习的主要挑战,来自于方差!。
过拟合 = 高方差。
正则化
在解决回归过拟合中,我们选择正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题,除了一些算法本身作用之外(决策树、神经网络),我们更多的也是去自己做特征选择,包括之前说的删除、合并一些特征
在学习的时候,数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多,所以算法在学习的时候尽量减少这个特征的影响(甚至删除某个特征的影响),这就是正则化
注:调整时候,算法并不知道某个特征影响,而是去调整参数得出优化的结
L2正则化

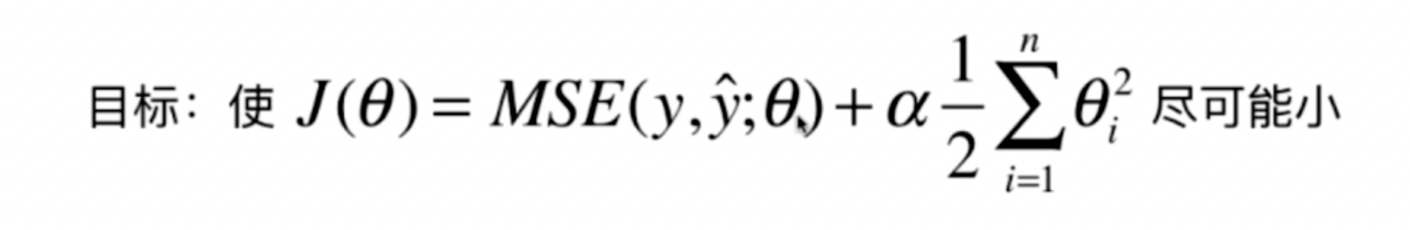
控制特征的Θ的值,让损失尽可能小。 原来的损失函数融合进 Θ的L2范数的平方。
使用L2正则化线性回归模型 就是 Ridge回归
1from sklearn.linear_model import Ridge
L1正则化

在损失函数中添加L1正则化项
alpha: 代表惩罚系数(正则化系数) , 后面是 n个参数w的 L1范数。也是个超参数。 越大惩罚越大。
使用L1正则化线性回归模型 就是 LASSO回归
1from sklearn.linear_model import Lasso
LASSO趋向于使得一部分theta值变为0 。所以可以作为特征选择用。
L0正则化
就是 让Θ个数 尽可能的少, 但是这种一般不用,是np难度 ,用L1代替正则化。
弹性网Elastic Net
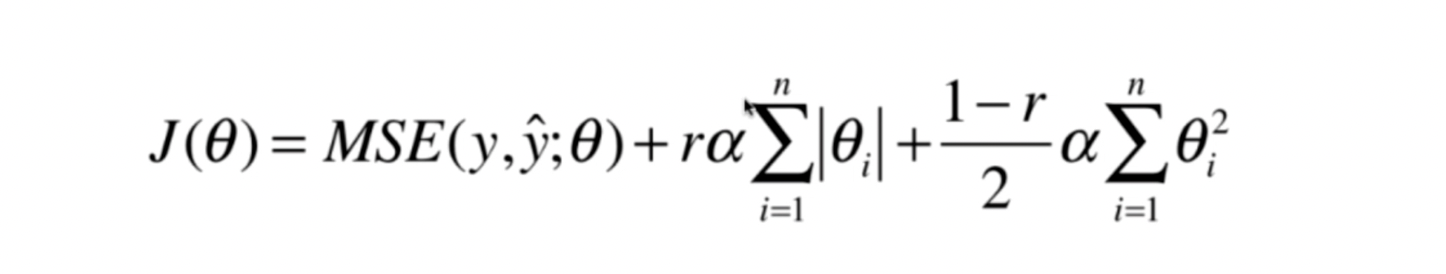
是岭回归和LASSO回归 结合。
L2正则化需要的计算能力更高点,退而求其次可以用这个 弹性网。
梯度下降法
梯度下降法是一种基于搜索的最优化方法,作用:最小化一个损失函数。
梯度上升法: 最大化一个效用函数。
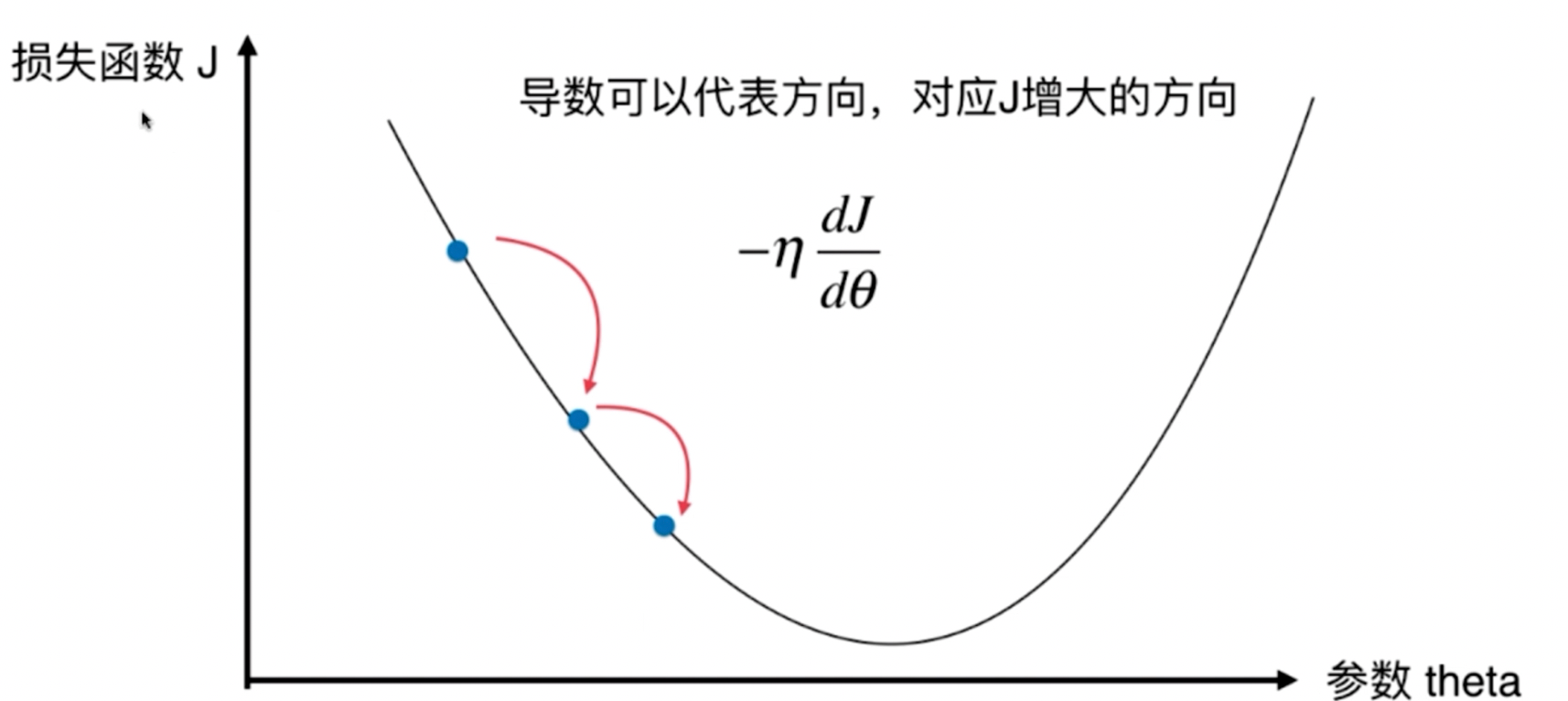
上图在抛物线的底端的左边,导数是负数,就是模拟增加theta,J向底端靠近,如果是在右边导数是正数,就是模拟减小theta,J也会向底端靠近
什么是梯度(gradient grad)
- 单变量中,梯度就是某一个点的切线斜率(某一点的导数),有方向为函数增长最快的方向
- 多变量函数中,梯度就是某一个点的偏导数;有方向:偏导数分量的向量方向
- 多元函数中的参数求Θ 偏导数,偏导数以向量的形式写出来,就是梯度;比如 J(Θ1,Θ2,Θ3)->偏导(dJ/dΘ1,dJ/dΘ2,dJ/dΘ3)
- 梯度就是导数+方向
梯度下降公式:
- 循环迭代求当前点的梯度,更新当前的权重参数Θ
- Θ_(i+1)=Θi - η * (dJ/dΘi)
- η 就是学习率,机器学习中0.001-0.01,深度学习中10^-6
- 梯度是上升最快的方向,需要下降就加个负号.
移动步长 : -η (eta)
- η 称为学习率
- η的取值影响获得最优解的速度
- η的取值不合适,甚至得不到最优解
- η是梯度下降法的一个超参数
调参 ,就是调η 。
- 局部最优解、全局最优解。
- 并不是所有函数都有唯一的极值点 (一会下降一会上升再下降上升等)
- 解决方案
- 多次运行,随机初始化点
- 梯度下降法的初始点也是个超参数。
- 解决方案
线性回归法的损失函数具有唯一的最优解。
模拟梯度下降法
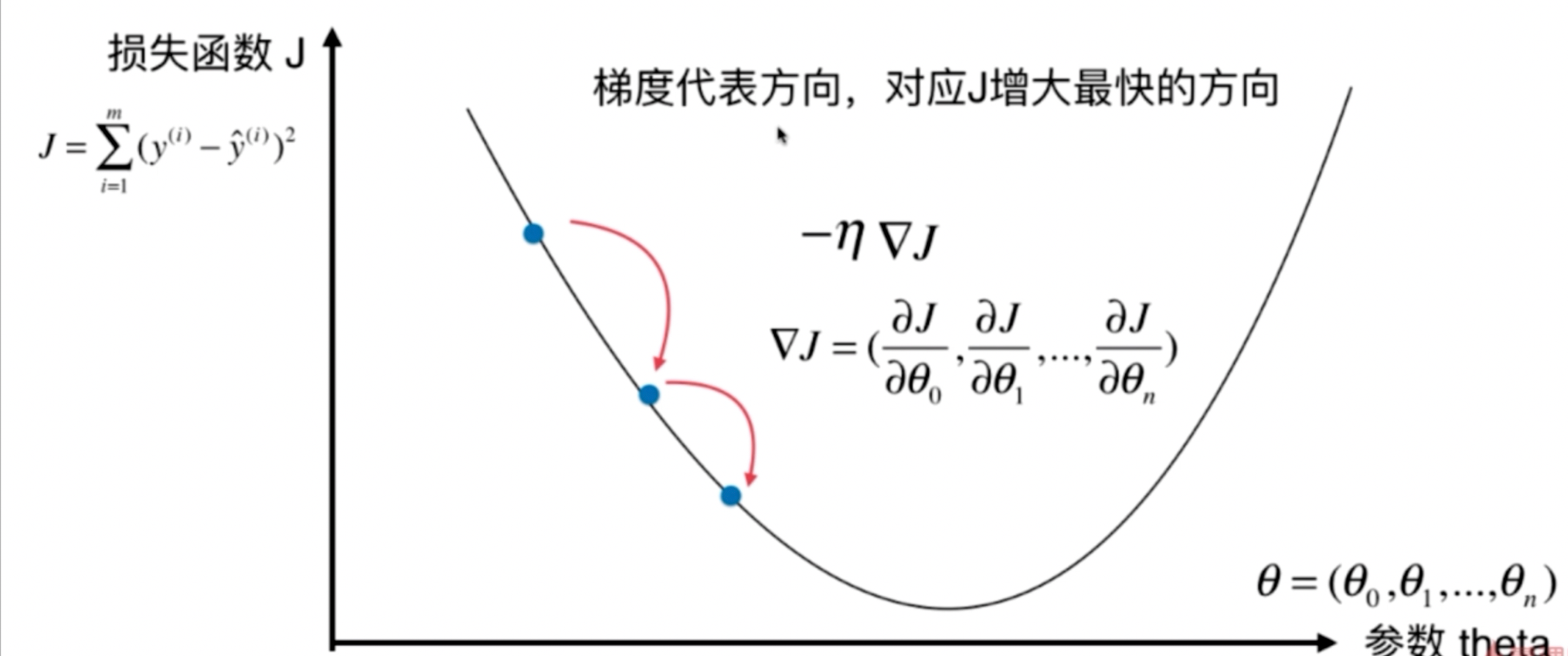
线性回归中的梯度下降法
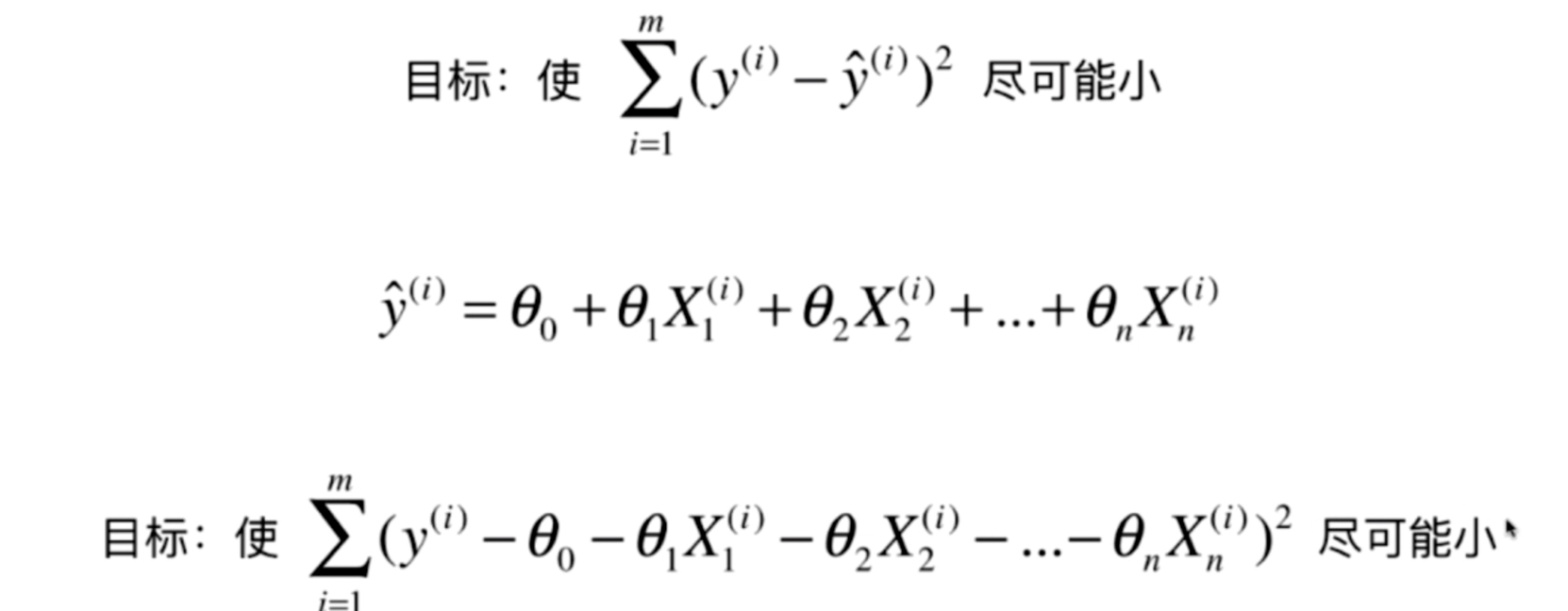

这么看m如果越大,损失就越大。 在梯度中是不合理的。 我们统一除以m,排除这个因素

梯度下降法实现
1# 求均方差,mes , theta 是一个数组,X_b 是一个矩阵 ,n行i列, n=len(X_b)
2def J(theta, X_b, y):
3 try:
4 return np.sum((y - X_b.dot(theta))**2) / len(X_b)
5 except:
6 # 异常则给 浮点数中的最大值
7 return float('inf')
8
9# 求导 (也就是损失值、梯度), 就是上图中的三角形J(theta)
10def dJ(theta, X_b, y):
11 res = np.empty(len(theta))
12 # 上图第0行有点特殊
13 res[0] = np.sum(X_b.dot(theta) - y)
14 for i in range(1, len(theta)):
15 # X_b[:,i] 代表, 第几列
16 res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
17 return res * 2 / len(X_b)
18
19
20# 求梯度下降中的 最优theta
21# initial_theta 初始化theta
22# n_iters 迭代次数控制
23# eta 学习率
24# X_b 矩阵
25# y 结果值
26# epsilon 接受的误差值
27def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
28
29 theta = initial_theta
30 cur_iter = 0
31
32 while cur_iter < n_iters:
33 # 下降梯度
34 gradient = dJ(theta, X_b, y)
35 last_theta = theta
36 theta = theta - eta * gradient
37 if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
38 break
39
40 cur_iter += 1
41
42 return theta
上面公式转成向量化运算方式
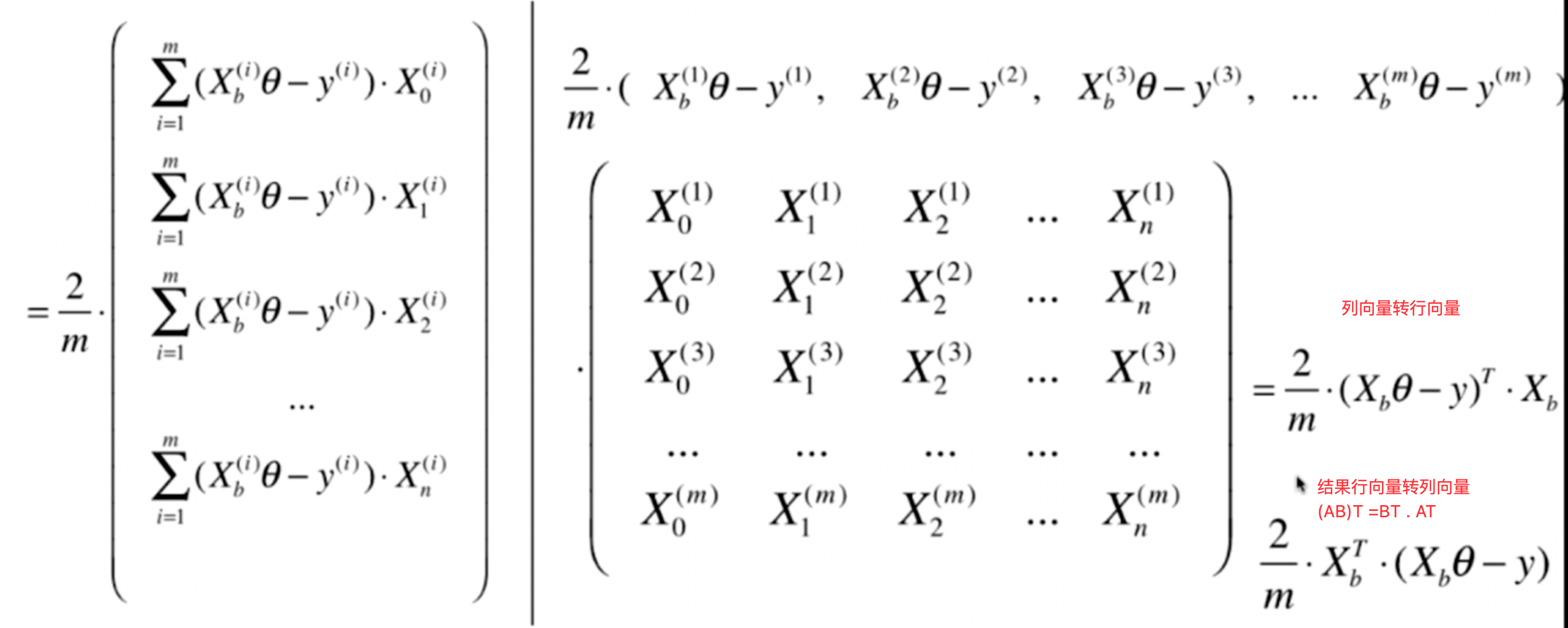
公式变成了 2个矩阵相乘
(1行,m列) 的行向量 乘 (m行,n+1列矩阵)
注意要把列向量转乘行向量,默认为列向量
新的梯度公式
1def dJ(theta, X_b, y):
2 # 公式
3 return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
利用梯度下降中,eta值要小,过大会导致得不到结果不收敛,太小导致,运行时长太长了
数据还要做归一化
使用梯度下降法寻找最小损失值的时候,数据要做归一化处理。
在数据集中,梯度下降法比正规方程 解线性回归要快很多。
随机梯度下降法
上面的梯度是对所有样本m 进行 梯度计算(也叫批量梯度下降法)。 如果m 很大,那么 这个算法可能也是很费时的。
随机梯度下降算法(SG), 这里是取一个样本,公式变乘下图所示

模拟退火的思想
学习率 = t0/ (i_iters (迭代次数) +t1)
经验值t0=5, t1=50
学习率逐渐变小
1# 求随机梯队, 公式
2# X_b_i X_b中的 第i个样本 只有一行记录
3def dJ_sgd(theta, X_b_i, y_i):
4 return 2 * X_b_i.T.dot(X_b_i.dot(theta) - y_i)
5
6def sgd(X_b, y, initial_theta, n_iters):
7 # 经验值
8 t0, t1 = 5, 50
9 # 学习率 随着迭代次数(时间) ,慢慢变小。
10 def learning_rate(t):
11 return t0 / (t + t1)
12
13 theta = initial_theta
14 for cur_iter in range(n_iters):
15 rand_i = np.random.randint(len(X_b))
16 gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
17 theta = theta - learning_rate(cur_iter) * gradient
18
19 return theta
梯度下降法相对好的做法
迭代所有样本 n次循环, 默认是5,然后循环的时候 每个样本都随机打乱,并且每一轮数据都要取到
梯度下降法调试手段
点的梯度 = 2点间, 无限趋近与0 的斜切率。
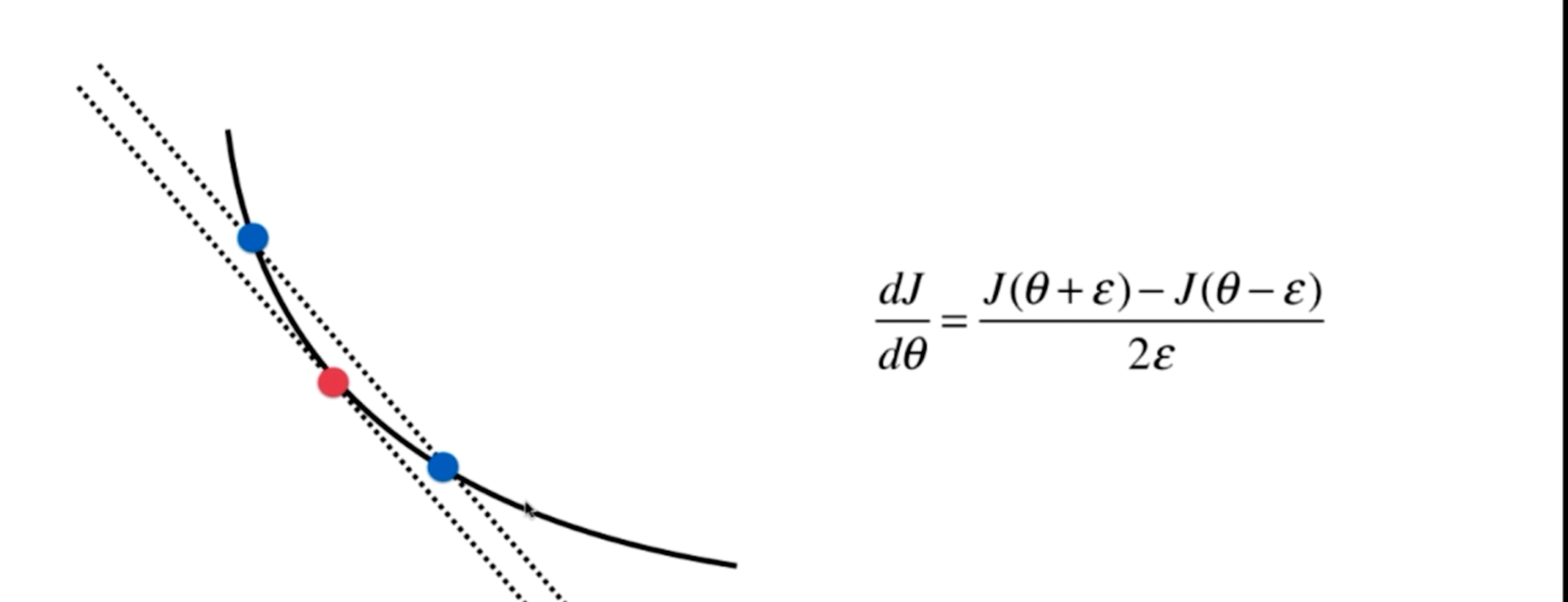
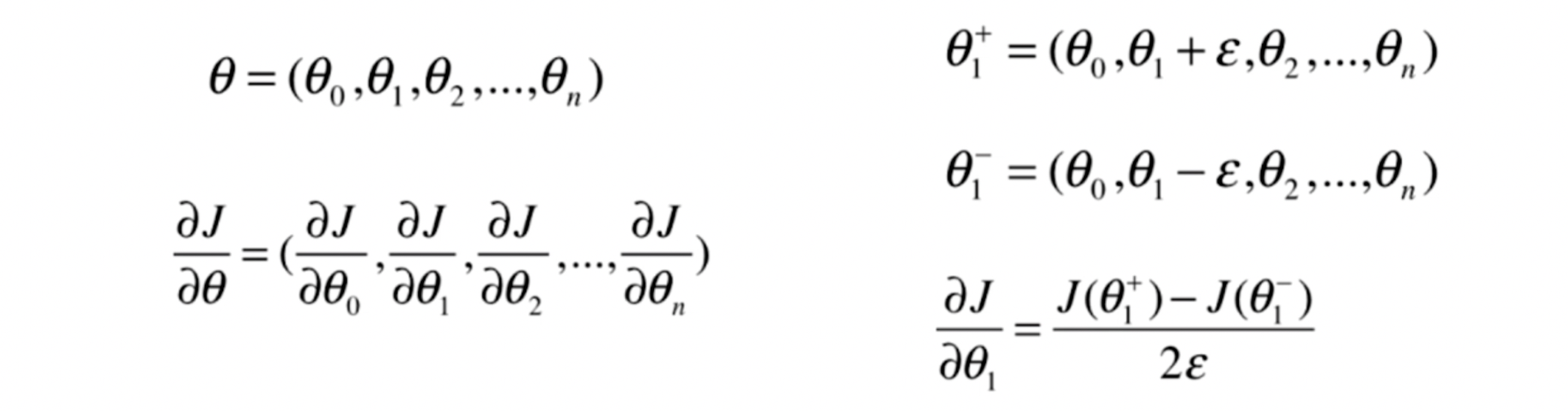
1# 损失值
2def J(theta, X_b, y):
3 try:
4 return np.sum((y - X_b.dot(theta))**2) / len(X_b)
5 except:
6 return float('inf')
7
8# 梯度debug,看看自己写的方式 和这个debug方式结果差,看是否正确 ,debug方式性能较慢,可以把这个方法加入到自己的工具箱中
9def dJ_debug(theta, X_b, y, epsilon=0.01):
10 res = np.empty(len(theta))
11 for i in range(len(theta)):
12 theta_1 = theta.copy()
13 theta_1[i] += epsilon
14 theta_2 = theta.copy()
15 theta_2[i] -= epsilon
16 res[i] = (J(theta_1, X_b, y) - J(theta_2, X_b, y)) / (2 * epsilon)
17 return res
小批量梯度下降法
批量梯度下降,是将所有样本看一遍才能求出梯度, 而随机梯度下降法,是看一个样本求出梯度。批量的求解慢,但是稳定,会朝着正确下降梯度走。而随机梯度下降法就是不稳定,甚至可能向反方向前进。
小批量,多大批量就是个超参数。
逻辑回归
逻辑回归是解决二分类问题的利器
应用场景
- 疾病是否是阳性
- 银行卡房贷款是否放贷
- 预测广告点击率(是否点击,是否推荐这个广告)
- 是否是垃圾邮件
- 推荐系统中用到很多二分类任务
极大似然估计
核心思想:
设模型中含有待估参数w,可以取很多值。已经知道了样本观测值,从w的一切可能值中(选出一个使该观察值出现的概率为最大的值,作为w参数的估计值,这就是极大似然估计。(顾名思义:就是看上去那个是最大可能的意思)
假设有一枚不均匀的硬币,出现正面的概率和反面的概率是不同的。假定出现正面的概率为𝜃, 抛了6次得到如下现象 D = {正面,反面,反面,正面,正面,正面}。每次投掷事件都是相互独立的。 则根据产生的现象D,来估计参数𝜃是多少?
1P(D|𝜃) = P {正面,反面,反面,正面,正面,正面}
2 = P(正面|𝜃) P(正面|𝜃) P(正面|𝜃) P(正面|𝜃) P(正面|𝜃) P(正面|𝜃)
3
4=𝜃 *(1-𝜃)*(1-𝜃)𝜃*𝜃*𝜃 = 𝜃^4(1 − 𝜃)^2
5
6求此函数的极大值时,估计𝜃为多少
1对上面函数求导
24𝜃^3.(1-𝜃)^2+ 𝜃^4. 2(1-𝜃)*-1
3= 4𝜃^3.(1-𝜃)^2 - 2𝜃^4(1-𝜃)
4
5= 𝜃^3.(1-𝜃)( 4-4𝜃 ) - 𝜃^3.(1-𝜃)(2𝜃)
6= 𝜃^3.(1-𝜃)(4-6𝜃 ) = 0
7
8𝜃1=0 ,𝜃2=1,𝜃3=2/3
9因为0,1不可能,所以𝜃 取2/3
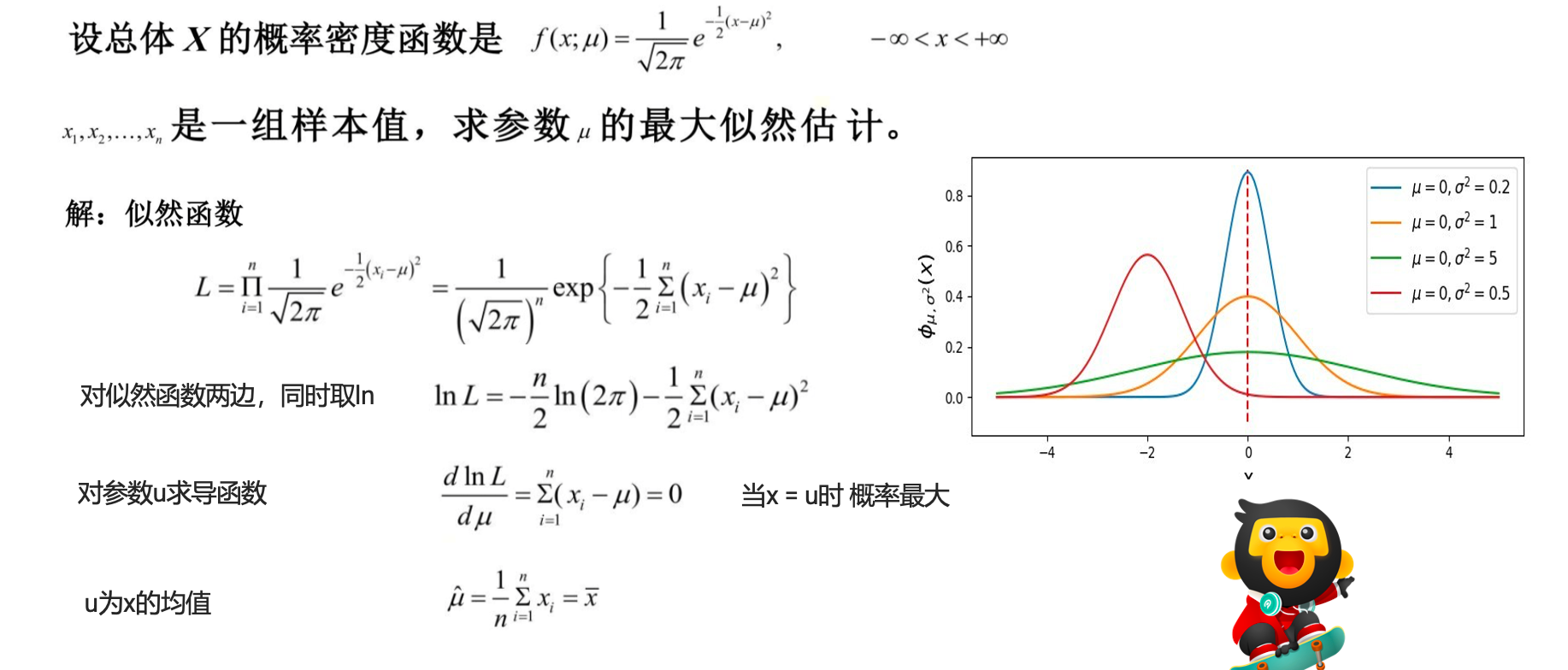
1ln(1/a)=ln(a^-1)=-lna
2ln(1/2π^(n/2)) = - ln 2π^(n/2) =-n/2 ln 2π
逻辑回归的原理
基本思想
-
利用线性模型 f(x) = wx + b 根据特征的重要性计算出一个值
-
再使用 sigmoid 函数将 f(x) 的输出值映射为概率值
- 设置阈值(eg:0.5),输出概率值大于 0.5,则将未知样本输出为 1 类
- 否则输出为 0 类
-
逻辑回归的假设函数
- h(w) = sigmoid(wx + b )
- 线性回归的输出,作为逻辑回归的输入
逻辑回归中,其输入值是什么
- 逻辑回归的输入就是一个线性方程
- h(w) = w1x1 + w2x2 + …. + b
如何判断逻辑回归的输出
- sigmoid函数
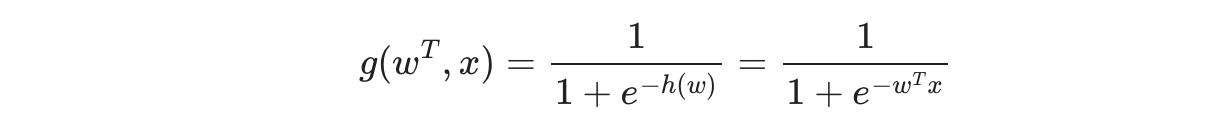
判断标准
回归的结果输入到sigmoid函数当中 输出结果:[0, 1]区间中的一个概率值,默认为0.5为阈值
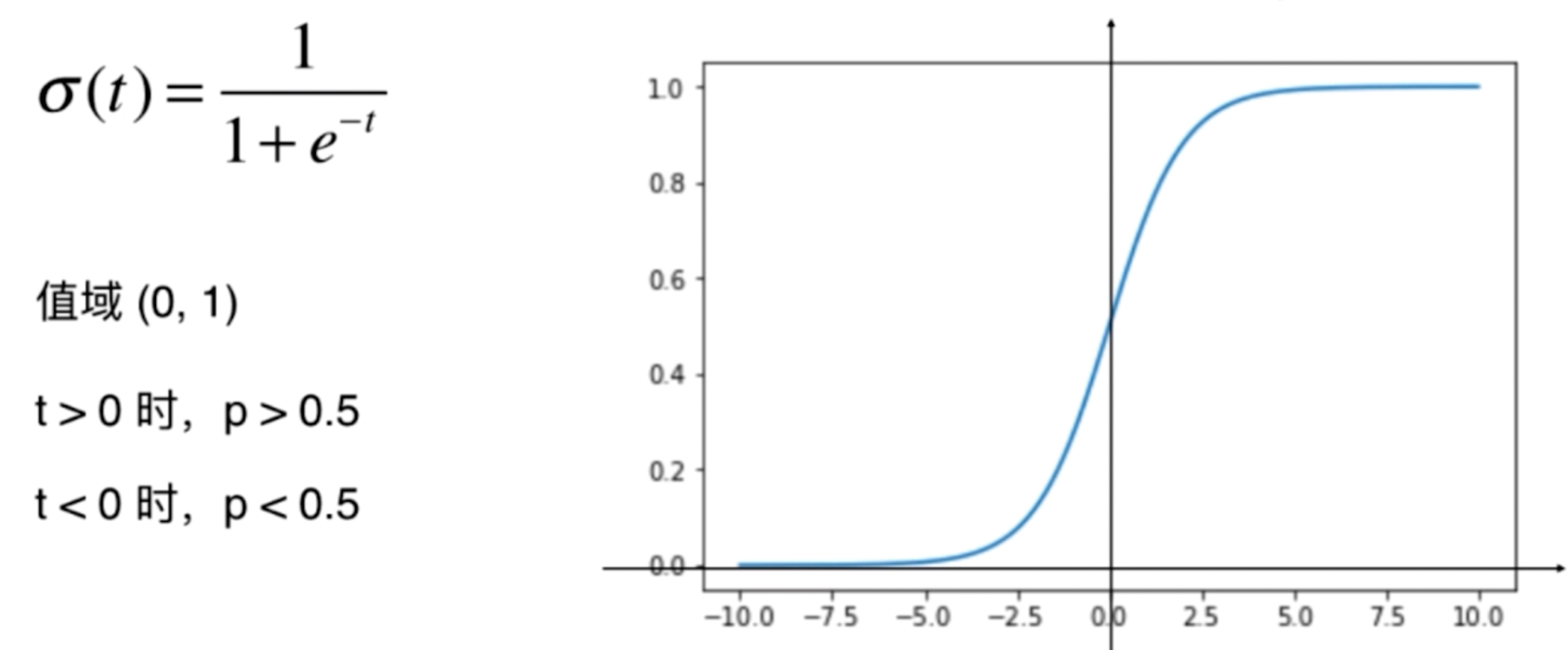
sigmod函数可导,是单调递增函数。
导函数公式: f’(x) = f(x) (1-f(x))
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)。(方便损失计算)

损失函数
其损失函数通常是对数损失函数(log loss),也称为交叉熵损失函数(cross-entropy loss)。对于逻辑回归模型,损失函数的定义如下:

- 一个样本
- 假设有2个类别,1的类别概率是p, 0的类别概率是1-p
1L = {
2 p if y = 1
3 1-p if y = 0
4}
5样本是1的概率是p,样本是0的概率是1-p
6
7上面等价于这个公式
8L = p^y . (1-p)^(1-y)
- n个样本
1L = (p1^y1 . (1-p1)^(1-y1)) * (p2^y2 . (1-p2)^(1-y2)) * .... * (p2^yn . (1-p2)^(1-yn))
2pi 为 每个样本 被分类正确时的概率
3yi 为表示每个样本的真实类别
- 对上面公式求对数转换公式
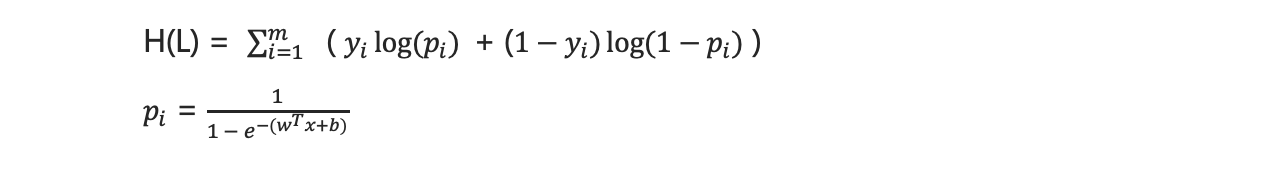
让联合概率最大时,估计w,b的参数,就是极大拟然估计
最大化问题变成最小化
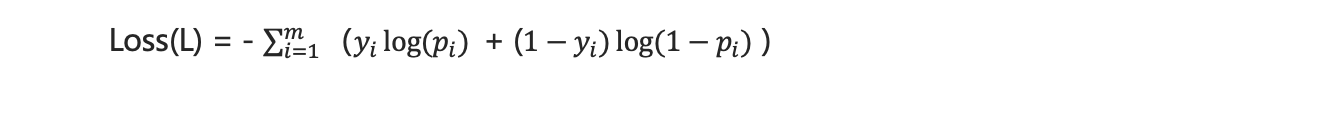
- 使用梯度下降算法,更新逻辑回归算法的权重参数
PCA
pca: 主要成分分析
-
一个非监督的机器学习算法
-
主要用于数据的降维
-
通过降维,可以发现更便于人类理解的特征
-
其他应用:可视化;去噪
-
如何找到样本间间距最大的轴
-
如何定义样本间间距
- 使用方差,方差大区分度大 (降维后区分度要大才好)
二维示例:
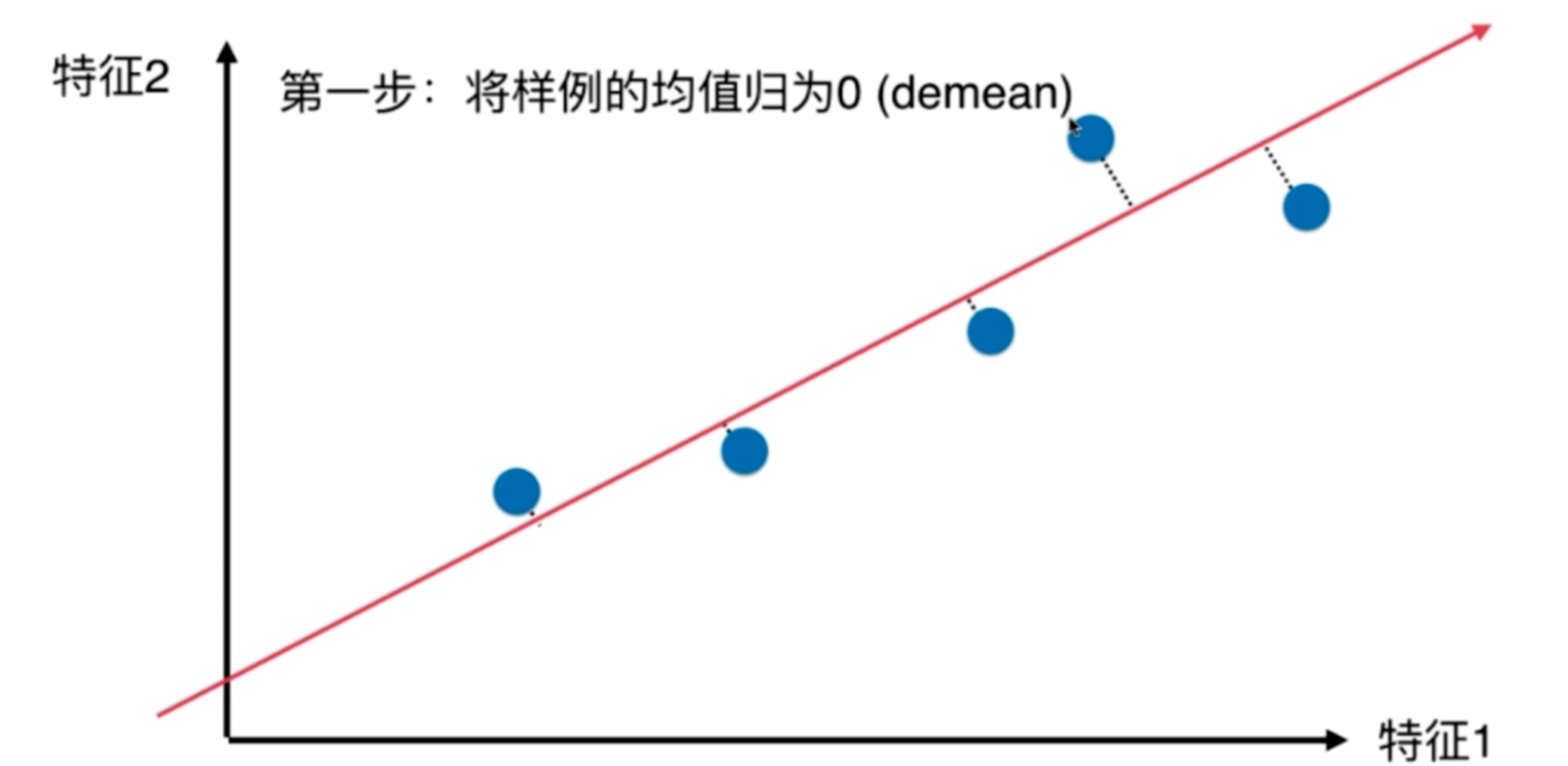
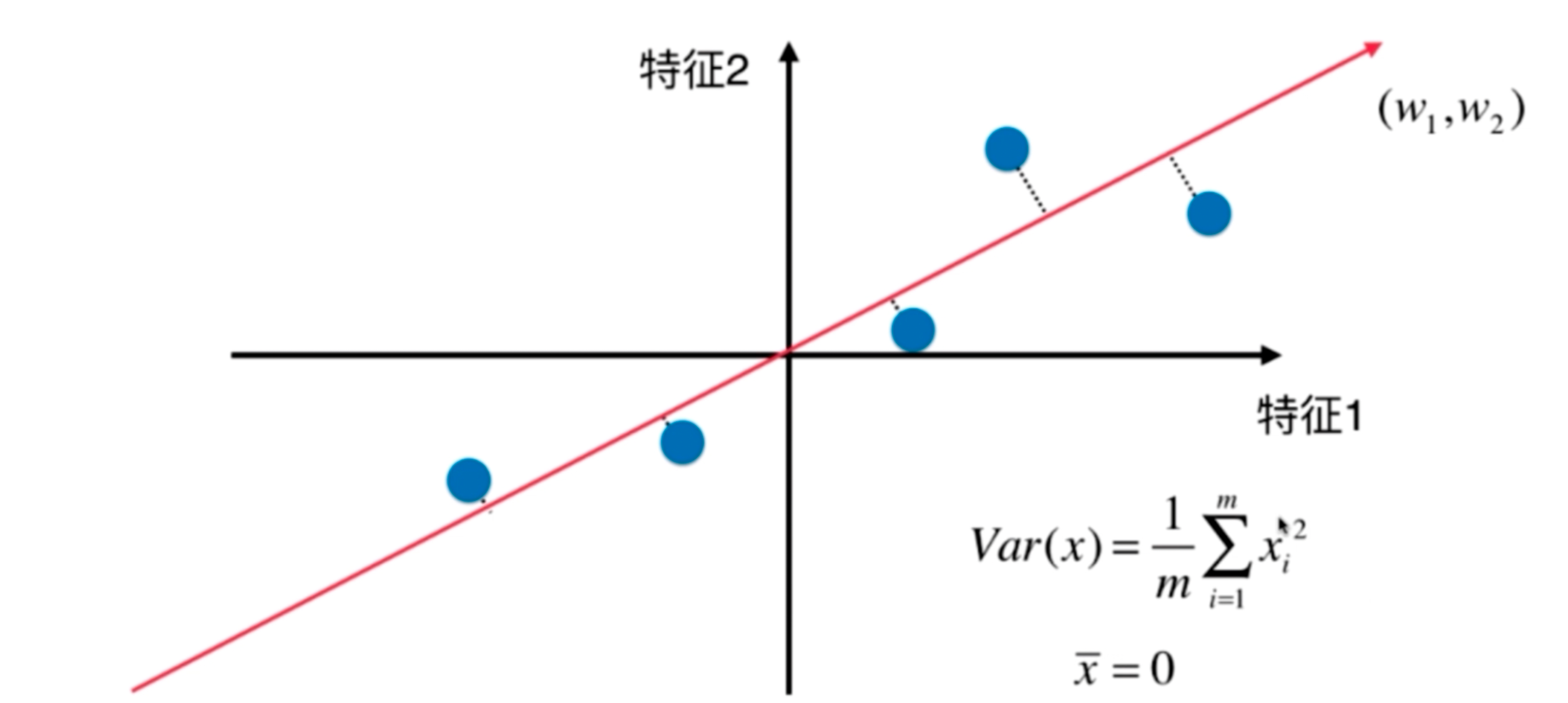
- 对所有的样本进行demean处理 (减去平均值)
- 我们想要求一个轴的方向 w=(w1,w2)
- 使得我们所有的样本映射到w以后,有
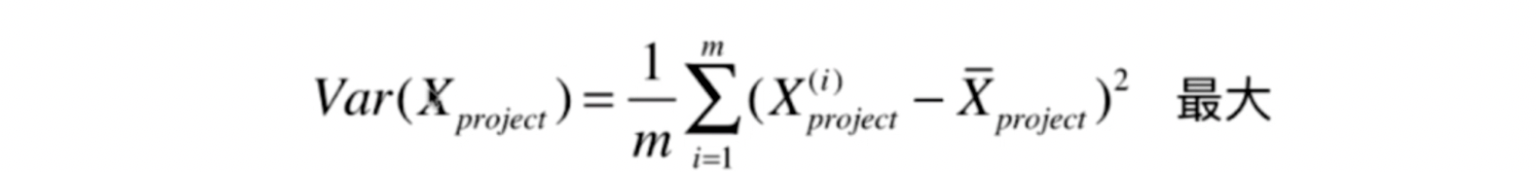
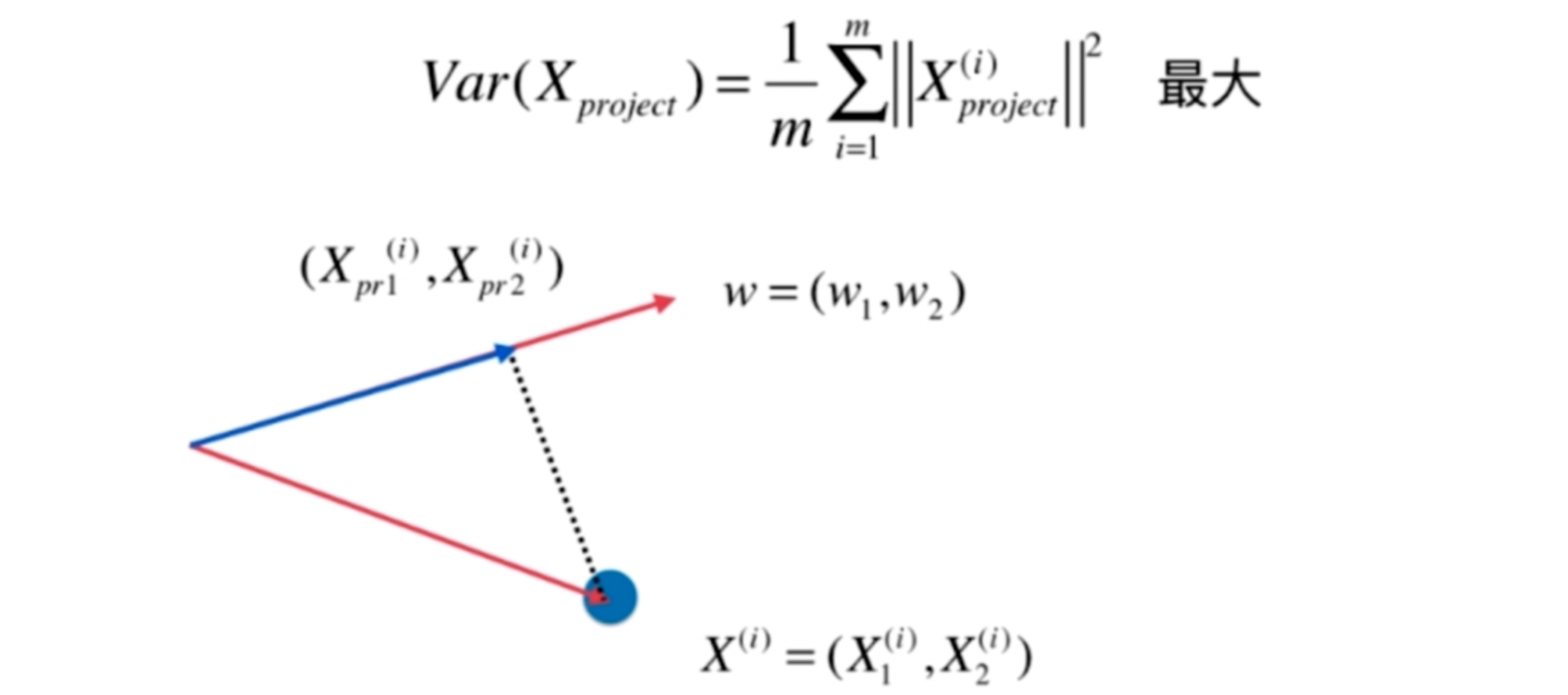
1向量的点乘=向量的模 * 向量的模 * cosΘ
2X(i).w = ||X(i)|| . ||w|| .cosΘ
3
4w为方向向量 ? ,它的模=1
5
6X(i).w = ||X(i)|| .cosΘ
7
8X(i).w = ||X_project(i)||
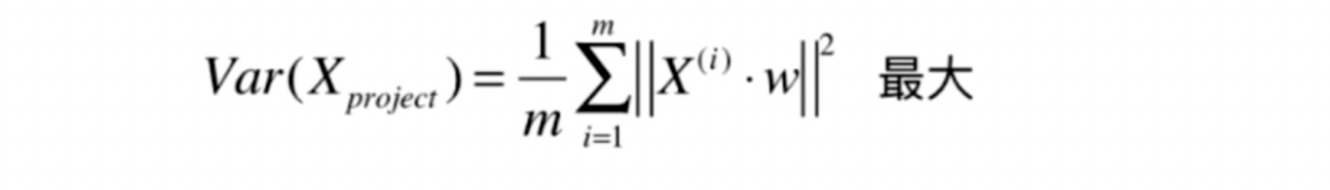

一个目标函数的最优化问题,使用梯度上升法解决

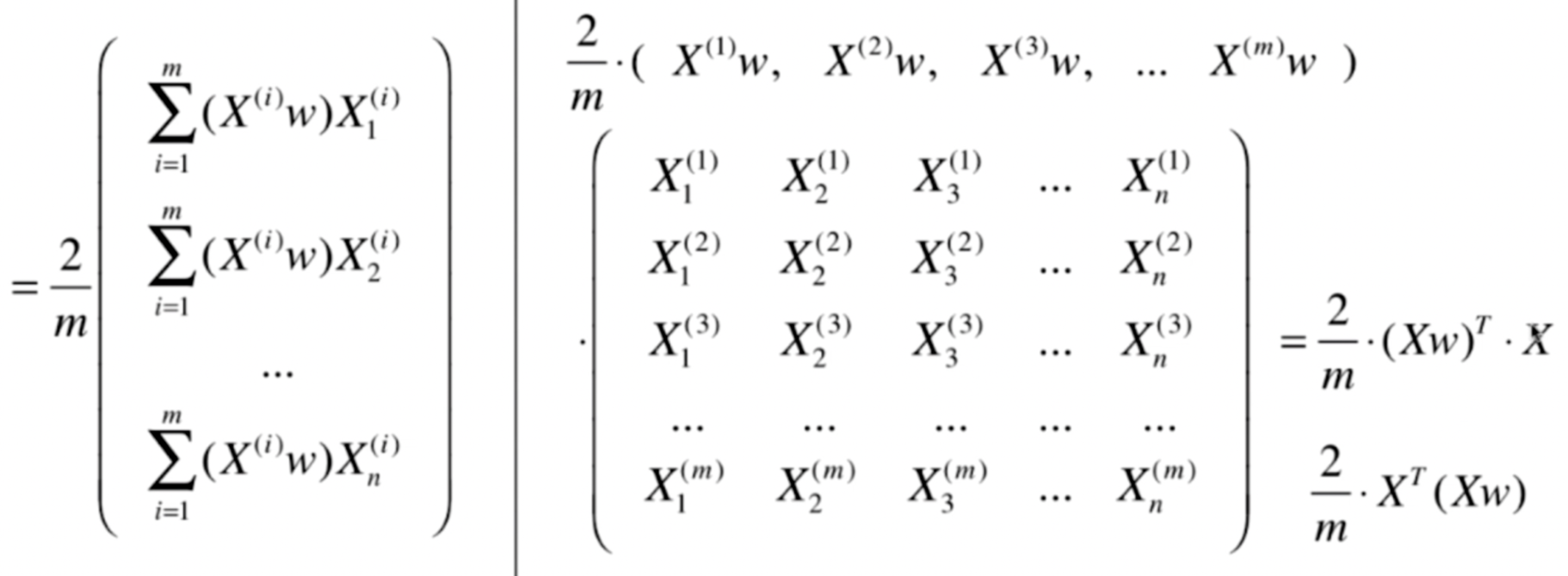
结果是 多行1列的 矩阵。所以有了最后一步: 1行多列的矩阵还要进行一次转置。