集合、映射和函数
集合
集合列子:
- 某特定时间上,某城市的树的种类
非集合例子
- 100个同批次同型号的乒乓球。 无法区别(元素互异性)
集合中的元素是坐标系中的点
- {(x,y)|x+y<3}
集合有包含关系。 子集: 所有元素都是 某集合。记作 A ∈ B
真子集( 集合不相等)
数集分类
- N 自然数集 N={0,1,2,3,…,n…}
- Z 整数集合 Z ={…,-n,…,-2,-1,0,1,2,…,n,….}
- Q 有理数集合
- R 实数集合 R = {x| x是有理数或无理数}
N ∈ Z, Z∈Q ,Q ∈ R
全集和补集
在实数集R中,集合A={x|0<x<=1} 的余集(补集) 就是 A^c = {x|x<=0或x>1}
区间
{x|a<x<b},称为开区间,记作(a,b)
{x|a<=x<=b} ,成为闭区间,记作[a,b]
领域
点a的领域记作 U(a)
设η是任一正数,则开区间(a-η,a+η) 就是a的一个领域,这个领域称为点a的η领域,记作U(a,η)
U(a,η) = {x|a-η <x < a+η}
映射
设A、B是两个非空集合,如果存在一个法则f:A->B,使得对于任意a∈A,都有f(a)∈B,则称f为A到B的映射。记作f:A→B。
b 称为元素a在映射 f 下的像, 记为 b = f(a)。
a 称为元素 b在映射 f 上的原像
集合A称为映射f的定义域,记作 D(f)
集合A中所有元素的像所组成的集合称为映射f的值域,记作 R(f)或者f(A)
- 映射三要素: 定义域,值域,对应法则
- 定义域 D(f) = A
- 值域 R(f) ∈ B
- 对于每个 a ∈ A ,元素 a 的像 b 唯一
- 对应每个b ∈ R(f) ,元素 b 的原像不一定唯一。
满射: Rf=Y
单射: ψ(任意符号)x,x2 ∈ X,x1!=x2,有f(x1) != f(x2)
一一映射: 满射+单射
逆映射
- 设f 是 A到B 的双射,那么存在一个映射 g:B→A,使得g(f(a))=a,g(b)=f(g(b))
对每个 b ∈ B ,规定g(b) = a, 这 a 满足f(a)=b
g 称为 f 的逆映射。记为 g=f-¹,定义域 D(g) = B, 值域 R(g) = A
函数
设数集D ∈ R ,则称映射f : D → R 为定义在 D上的函数。记为 y=f(x),x ∈ D,x 称为自变量,y 称为因变量, D称为定义域
反函数
设映射 f: D->E为双射(D∈R,E∈R)
则它的逆映射 f-¹ : E->D称为 f 的反函数。
f(x)=x²
f-¹(x)=sqrt(x)
函数的特性
函数单调性
函数奇偶性
奇函数: f(x)=-f(-x) ,图像关于原点对称
偶函数: f(x)=f(-x) ,图像关于 y 轴对称。
函数的周期性: x∈D,且(x+l)∈D ,f(x+l)=f(x) 恒成立,则f(x)为周期函数。如正弦、余弦函数,周期2π。
基本初等函数
- 幂函数 y=x^n (n∈R ,常数)
- 指数函数 y=a^x (a>0,且 a!=1)
- 对数函数 y=log_a(x) (a>0,且 a!=1)
- 三角函数 y=sin(x) ,y=cos(x) ,y=tan(x)等
- tan(x) =sin(x) / cos(x)
- 反三角函数 y=arcsin(x)、y=arccos(x)、y=arctan(x)等
一次函数
二次函数
- y=ax²+bx+c
- 对称轴: -b/2a
- a > 0 开口向上 ,(-♾️,-b/2a) 单调递减. (-b/2a,+♾️) 单调递增 ,最小值 (4ac-b²)/4a
- a < 0 开口向下 ,(-♾️,-b/2a) 单调递增. (-b/2a,+♾️) 单调递减 ,最大值 (4ac-b²)/4a
二次函数简单应用实例
-
桥梁建筑设计
-
篮球、排球落点
-
经济学的投资分析,售价定价
-
某商品进价 80元,按 100元出售,一天可卖 60件,经时长调查,该商品每降价 1 元,销量增加 5 件,求该商品售价多少,利润最大。
设定 商品售价x,每天售出为60+5(100-x)
y= (x-80)*(60+5(100-x)) = -5x^2+960x-44800
当 x=96时,y 取得最大值。
对数函数
y=log_a(x) (a >0, a!=1)
常用公式
log_a(x1)+log_a(x2) =log_a(x2*x1) , log_2(4)+log_2(8) = log_2(32)=5
log_a(x1)-log_a(x2) =log_a(x1/x2), log_2(4) -log_2(8) = log_2(1/2) = -1
log_a^m (x^n) =n/m log_a(x) , log_2^3(8^2) = 2/3 log_2(8)= 2
log_a(x) = log_b(x)/log_b(a) ,log_32(64) = log_2(64) / log_2(32) = 6/5
正弦函数
y=a*sin(ωx+φ) a(a>0) 振幅,w 频率, φ初始相位
傅里叶级数
应用:通信、电子等和电有关的领域。
最小正周期 T = 2π/ω ,有界 y∈[-|a|,|a|]
对称轴处取得极值
wx+φ=π/2 +2kπ , 取得极大值,k ∈ Z
wx+φ=-π/2 +2kπ ,取得 极小值,k ∈ Z
余弦函数
y=a * cos(wx+φ) , a(a>0) 振幅,w 频率, φ初始相位
物理应用领域。
最小正周期 T = 2π/ω ,有界 y∈[-|a|,|a|]
wx+φ=2kπ, 取得极大值,k ∈ Z
wx+φ=π+2kπ, 取得极小值,k ∈ Z
参数方程
x=2t
y = 3t^2 ,去除参数 t
得到 y=3/4x^2,二者等价
极坐标系
x=rcosθ,
y=rsinθ
描述与角度有关的曲线会更简洁
数列极限
数列
将自然数按1,2,3…编号依次排列的一列数x1,x2,x3,…,xn称为无穷数列,简称数列。
xn称为通项,此数列可以记为:{xn}
例如2,4,8,16… 记为: {2^n}
- 如果对于任意给定的正数ε(不论有多么小),
- 总存在正整数N,
- 使得对于n > N时的一切xn,
- 不等式|xn-a| < ε都成立
那么就称常数a 是数列xn的极限,或者称数列xn收敛于a.
记为: 数列xn 当n接近无穷大时,数列的极限是a。
1lim xn=a (或 xn->a(n->∞))
2n->∞
如果数列没有极限,就说数列是发散的,否则是收敛的。
1lim xn=a <=> ∀ε > 0 ,∃ 正整数N,当n>N时,有|xn - a| < ε
2n->∞
- ∀表示任意给定的或对于每一个
- ∃ 表示存在或至少有一个
- 数列极限的定义未给出求极限的方法
收敛数列的性质
- 有界性
- 唯一性,,每个收敛数列只有一个极限.
函数极限
函数的极限:在自变量的某个变化过程中,如果对应的函数值无限接近于某个确定的数,那么这个确定的数就叫做在一一变化过程中的函数的极限。
- 如果对于任意给定的正数ε(不论有多么小),
- 总存在正数δ,使得对于合适不等式0<|x-x0|<δ的一切x
- 所对应的函数值f(x)都满足不等式|f(x)-A| <ε,
- 那么常数A就叫做函数f(x)当x->x0时的极限
1lim f(x)=A <=> f(x)->A(当x->x0)
2x->x0
1lim f(x)=A <=> ∀ε > 0 ,∃ δ>0,当0<|x-x0| < δ时,恒有|f(x)-A| < ε
2x->x0
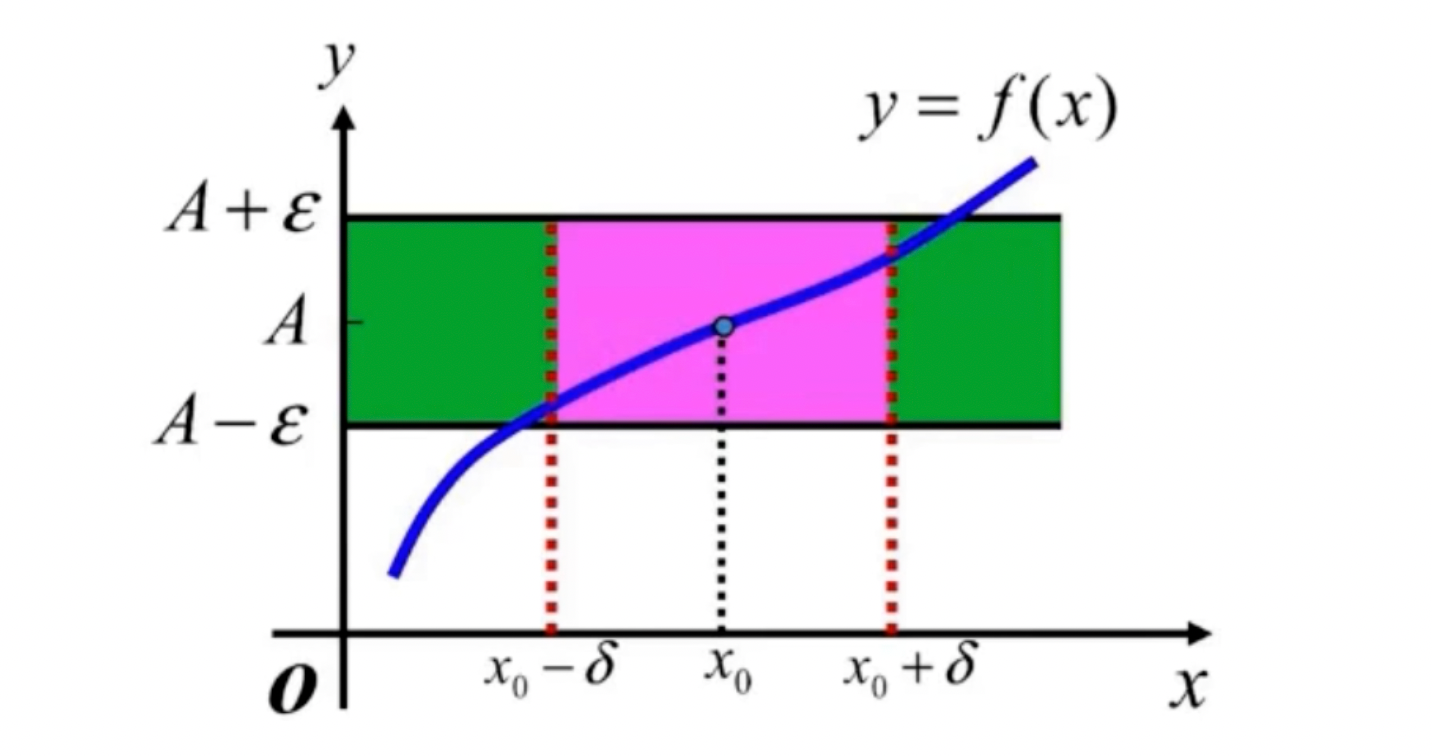
当x在x0的δ去心领域时,函数y=f(x)图形完全落在以直线y=A,带宽为2 ε 的区域内
- 函数极限与f(x)在x0是否有定义无关。(x0 是否在定义域内没有关系)
- δ与任意给定的正数ε相关
- 找到一个δ后,δ越小越好,它体现x与x0的接近程度。
单侧极限
左极限
1 ∀ε > 0 ,∃ δ>0,当x0-δ<x<x0 ,恒有|f(x)-A| < ε
2记作 lim f(x) =A <=> f(x0-0)=A
3 x->x0-
右极限
1 ∀ε > 0 ,∃ δ>0,当x0<x<x0+δ ,恒有|f(x)-A| < ε
2记作 lim f(x) =A <=> f(x0+0)=A
3 x->x0+
自变量无穷大函数的极限
ε-X语言:
1lim f(x) =A <=> ∀ε > 0 ,∃ X>0,使当|x|>X时,恒有|f(x)-A| < ε
2x->∞
定理:
1lim f(x)=A <=> lim f(x)=A 且 lim f(x)=A
2x->∞ x->+∞ x->-∞
函数极限的性质
- 唯一性
1如果lim f(x)存在, 那么此极限唯一. 2 x->x0 - 局部有界性
极值
无穷小
极限为0的变量称为无穷小
无穷小量即以数0为极限的变量,无限接近于0。确切地说,当自变量x无限接近x0(或x的绝对值无限增大)时,函数值f(x)与0无限接近,即f(x)→0(或f(x)=0),则称f(x)为当x→x0(或x→∞)时的无穷小量。
特别要指出的是,切不可把很小的数与无穷小量混为一谈。
零时可以作为无穷小的唯一常数
记作:
1lim f(x)=0 或 lim f(x) = 0
2x->x0 x->∞
例:
1lim sinx=0 函数sinx是当x->0时的无穷小
2x->0
3
4
5lim 1/x =0 那么函数1/x 是当x->∞的无穷小
6x->∞
无穷小和函数极限的关系
定理1
1lim f(x) =A <=> f(x) = A+α(x),α(x)是当x->x0时的无穷小.
2x->x0
定理给出了函数f(x)在x0附近的近似表达式, f(x) ≈ A,误差为α(x)。
定理2: 有限个无穷小的和也是无穷小
定理3:有界函数与无穷小的乘积是无穷小
- 推理1 常数和无穷小的乘积是无穷小.
- 推理2 有限个无穷小的乘积也是无穷小.
无穷小
1 因为 lim(x-2)=0 ,所以函数(x-2) 为 x->2的时的无穷小
2 x->2
3
4 因为 lim(x-2)^2=0 ,所以函数(x-2)^2 为 x->2的时的无穷小
5 x->2
极限存在的充要条件
- 在自变量的同意变化中x->x0 或x->∞时,函数值f(x)具有极限 A的充要条件是f(x)=A+α,其中α是无穷小
- f(x)=1+1/x+2/x^2 =1+α(x)
1lim α(x) = lim(1/x+2/x^2) = 0
2x->∞ x->∞
3
4lim(1+ 1/x+2/x^2) = 1
5x->∞
无穷大
- 如果对于任意给定的正数M(不论有多大)总存在正数δ(或正数X),
- 使得对于合适不等式 0<|x-x0| <δ (或|x|>X)的一切x,
- 所对应的函数值f(x) 都满足不等式|f(x)| > M
- 那么称函数f(x) 当x->x0 (x->∞ ) 时为无穷大
记作:
1lim f(x) = ∞ 或 lim f(x)=∞
2x->x0 x->∞
定理:
- 在自变量的同一变化过程中,如果 f(x)为无穷大,那么1/f(x) 为无穷小。
- 如果 f(x)为无穷小,且f(x) !=0 , 那么1/f(x) 为无穷大。
**关于无穷大的讨论,都可归结于关于无穷小的讨论。 **
1正无穷大
2lim f(x) = ∞
3x->x0
4
5负无穷大
6lim f(x)= -∞
7x->x0
- 无界变量未必是无穷大
- 不可将 无穷大认为是 极限存在。
极限
极限就是研究自变量无限接近一个数或其绝对值无限增大时,函数值是否会无限接近一个数
lim 就是极限
极限运算法则
- 有限个无穷小之和 仍然是无穷小
- 有限函数与无穷小的积仍然是无穷小
- 有限个无穷小之积仍然是无穷小
- 如果lim f(x)=A ,lim g(x) =B
- lim f(x) +- g(x) = A+-B
- lim f(x) * g(x) = A*B
- lim f(x) / g(x) = A/B ,其中B!=0
- 如果 lim g(x) 存在,c 为常数,则 lim[c g(x)] = c lim g(x)
- 如果 lim g(x)存在,n 为正整数,则 lim [g(x)]^n=[lim g(x)]^n
- 有数列{a_n},{b_n} 如果 lim a_n=A, lim b_n=B, n->∞.
- lim(a_n + b_n) = A+B
- lim(a_n * b_n ) =A*B
- 当b_n!=0 (n=1,2,3….) 且 B!=0 时,lim (a_n/b_n) = A/B
夹逼准则
1|x| > M 时,g(x) <= f(x) <= h(x)
2
3lim g(x)=A ,lim h(x) =A
4x->x0 x->x0
5(x->∞ ) (x->∞ )
6
7那么函数f(x)的极限存在,则
8
9lim f(x)=A
10x->x0
11(x->∞)
柯西极限存在准则
数列{xn}收敛的充分必要条件: 对于任意给定的正数ε,存在着这样的正整数N,使得当m>N,n>N时就有 |xm-xn|<ε
极限存在准则
- 若数列{a_n} 、 {b_n}、{c_n} 满足从某项n_0开始起,当 n > n_0 时, a_n <= b_n <=c_n ,且 lim a_n = m ,lim c_n=m ,则{b_n}极限存在且 lim b_n = m
- 单调有界数列必有极限
- 两个重要结论
1lim(1+1/x)^x = e
2x->∞
3
4lim(1+y)^(1/y) = e
5y->0
6
7
8lim sin(x) /x = 1
9x->0
无穷小比较
- 若 lim b/a = 0 则 b 是比 a 高阶的无穷小,记为b=O(a)
- 若 lim b/a= ∞ 则 b 是比 a 低阶的无穷小
- 若 lim b/a=c, !=0 ,则 b 与 a 同阶无穷小
- 若lim b/a=1 ,则 b 与 a 等阶无穷小,记为a~b
- 若lim b/a^m = c ,!=0 ,m>0 ,则 b 是关于 a 的 m 阶无穷小。
log_a(e)= 1/ ln_a
常用结论
- log_a(1+x) ~ 1/ln_a . x
- ln(1+x) ~ x
- a^x -1 ~ ln_a . x
- e^x -1 ~x
- (1+x)^a -1 ~ ax
极限与函数连续性
- 某点处连续性判断,左极限=右极限=该点函数值
- 一切初等函数在其定义域区间内都是连续的
增量
- 变量u, 初值u1->终值u2
- 增量△u :△u=u2-u1
- 正的增量△u:u1变u2时是增大的
- 负的增量△u:u1变u2时是减小的
函数的增量
- 设函数f(x)在U(x0)内有定义
- ∀ x ∈ U(x0),△x=x-x0称为自变量在点x0的增量
- △y=f(x0+△x)-f(x0)称为函数f(x)相应于△x的增量.
连续的定义
- 设函数y=f(x)在点x0的某一领域内有定义
- 如果
1lim f(x)=f(x0)
2x->x0
那么就称y=f(x)在点x0 连续
ε-δ语言:
- ∀ ε>0,∃δ>0,
- 当|x-x0|<δ时,
- 恒有|f(x)-f(x0)|<ε.
左连续、右连续。
导数与微分
导数的定义
切线 y=f(x)=0.1x^2
割线斜率 = (f(x + h) - f(x)) / h
切线斜率:
1lim (f(x+h)-f(x))/h
2h->0
斜率绝对值越大,直线越陡峭
导数的定义

导数概念就是函数变化率这一概念的精确描述
1△y/△x : y在[x0,x0+△x ]的平均变化率
2
3f'(x): y在x0点处的变化率
4
5反应了因变量随着自变量的变化而变化的快慢程度
1导数 f'(x0) = lim (f(x0+h)-f(x0))/h , h->0
2所有点的导数构成导函数 f'(x) = lim (f(x+h)-f(x))/h , h->0
3导数是平均变化率的极限
4
5y=f(x) 的导数可以记为y'、f'(x) 、dy/dx、 df(x)/dx
可导与连续,可导一定连续
1 f'(x0) = lim (f(x0+h)-f(x0))/h , h->0
2 (f(x0+h)-f(x0))/h = f'(x0) +@(h)
3f(x0+h)-f(x0) = f'(x0)h+@(h)h
4
5lim |f(x0+h)-f(x0) | = lim | f'(x0)h+@(h)h | =0 ,h->0
导数充要条件:
1极限 lim (f(x0+h)-f(x) ) / h 存在的充分必要条件:左右极限都存在且相等
2 h->0
3
4 左导数: f'_(x0)
5 右导数: f'+(x0)
6
7 左导数=右导数
切线方程与法线方程
- 切线方程: y-y0=f’(x0)*(x-x0)
- 法线方程: y-y0= (-1/f’(x0)) * (x-x0)
- 法线的斜率 = -1/ 切线的斜率
函数的可到性与连续性的关系
可导必连续
1lim △y/△x = f'(x) 存在,因此必有△y/△x = f'(x)+α,其中 lim α=0
2△x->0 △x->0
3
4
5 △y=f'(x)△x+ α△x ,△x->0 , △y->0
6 所有函数f=f(x)在点x连续
f(x)在点x可导,那么在x点必连续。
y=|x| ,在x=0处连续,但不可导。
常见函数的导数

导数四则元算

求导
导数求极值:
- 导数为 0 的时候是函数的极值点
- 求函数 y=x^2 -4x +5 的极小值
求导法:对x求导,另 y’=2x-4 =0 ; x=2
y=1 就是极小值
高阶导数
变速直线运动 s=s(t)
速度v = ds/dt 或 v=s'
加速度 a=dv/dt = d (ds/dt)/dt 或 a=(s’)'
s对t的二阶导数,记作 d^2 . s / dt^2 或 s’’(t)
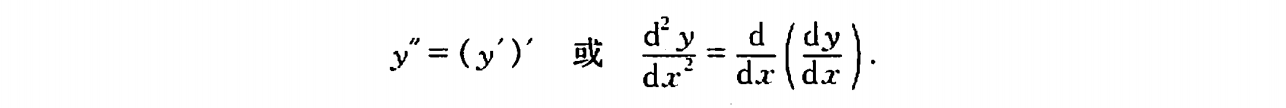
定义若函数y=f(x)的导数y’=f’(x) 可导,则称f’(x)的导数为f(x)的二阶导数,记作 y’’ , (y’)'
y’’’,y(4),y(n) n阶导数。
莱布尼茲公式
隐函数的导数


幂指函数求导法则
两边取对数(对数求导法)

参数方程所确定函数的导数
1{
2 x=F(t)
3 y= f(t)
4}
5
6dy/dx=f'(t)/F'(t)
微分中值定理
- 罗尔定理
- 拉格朗日中值定理
- 柯西中值定理
这3个定理,是层层递进的。
罗尔定理
- 在闭区间[a,b]上连续:确保函数在区间端点处也是连续的,没有间断。
- 在开区间(a,b)内可导:确保函数在该区间内可以进行求导运算。
- f(a)=f(b):确保函数在区间的两端取值相同。

推出: 在(a,b)内至少存在一个点ε,f’(ε)=0
拉格朗日中值定理
如果函数f(x)满足:
- 在闭区间上[a,b]连续;
- 在开区间(a,b)上可导;
- 那么在开区间(a,b)内至少存在一点ξ使得f’(ξ)=(f(b)-f(a))/(b-a)。
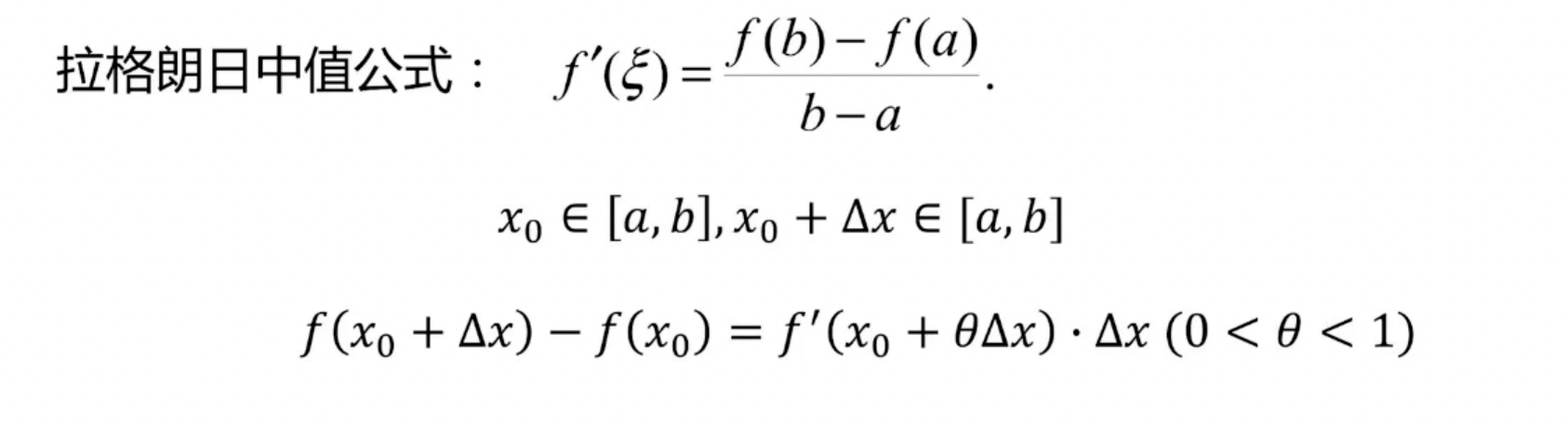
拉格朗日中值定理的有限增量形式: △y=f’(x0+Θ. △x) .△x (0<Θ<1)
函数的微分: dy=f’(x).△x , dy->△y(△x->0)
拉格朗日中值定理应用

ln1=0
柯西中值定理


偏导
多元函数求导, 把其他变量都看作常数
z是关于x和y的函数记成z(x,y) , z=(x-2)^2+(y-3)^2
1δz/δx = 2(x-2).1=0, x=2时可以在x方向求导极限值
2δz/δy = 2(y-3).1=0, y=3时可以在y方向求导极限值
1z=x^y
2δz/δx = y.x^(y-1)
3δz/δy = ln(x) . x^y
1z=e^(2x^2-3y)
2δz/δx =e^(2x^2-3y).(2x^2-3y)'=e^(2x^2-3y).4x = 4x.e^(2x^2-3y)
3δz/δy =e^(2x^2-3y).(2x^2-3y)'= -3e^(2x^2-3y)
links
- 高等数学第6版 上下册